TIEBitmap.AlphaChannel

Declaration

property AlphaChannel: TIEBitmap;

Description

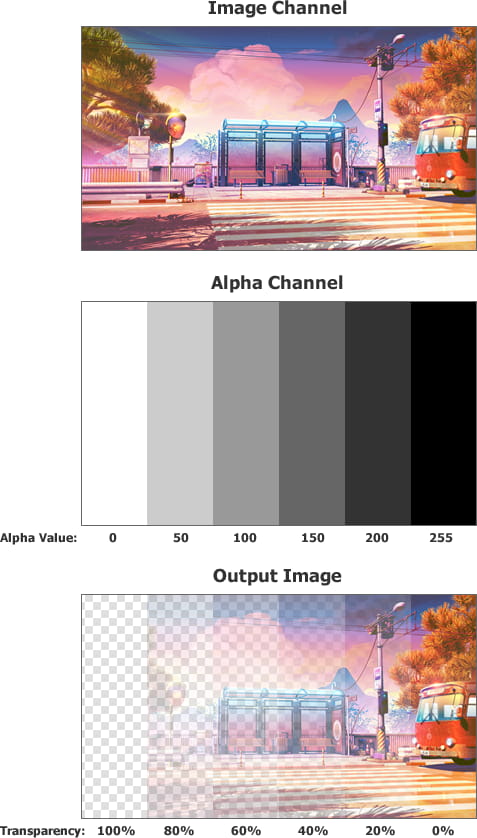
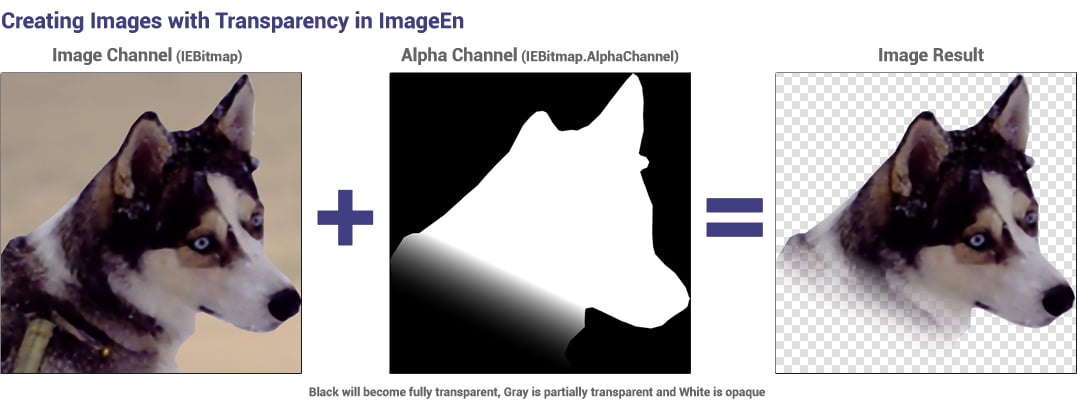
TIEBitmap handles the alpha channel as an encapsulated TIEBitmap object with pixelformat of ie8g. Pixels that are 0 (black) will be fully transparent, pixels of 255 are fully opaque, and values from 1 - 254 are partially transparent.
This property returns the associated AlphaChannel.
If an image doesn't have an alpha channel, you can create it just using AlphaChannel property.
To determine whether an image has an alpha channel and/or contains transparent regions, check HasAlphaChannel.

File Formats and Alpha

In order to maintain the alpha channel when saving, you will need to choose a format that supports it. The most widely used image format with true alpha support is PNG.

Alpha Channel is supported by:
- BMP, if BMP_HandleTransparency is enabled
- CUR
- ICO
- IEN
- JPEG 2000 with certain formats such as ioJ2000_RGB
- GIF, if GIF_FlagTranspColor is enabled
- PNG
- PSD
- SVG
- TGA
- TIFF (supported by some formats)
- WIC formats, such as HDP, WDP, HEIF, etc.
- WMF/EMF Metafiles (if EMFBackgroundColor = clNone)

It is not supported by: AVI, Camera RAW, DCX, DICOM, JPEG, PCX

Example

// Assign an alpha channel to an image using a source file
// For simple transparency, use a monochrome bitmap where the black pixels will become transparent
// Otherwise, a 256 color gray-scale image can provide a range of tranparency values (from white/fully opaque to black/fully transparent)
aBMP := TIEBitmap.create( 'D:\alpha.bmp' );

// Use our bitmap as the alpha channel
ImageEnView1.IEBitmap.AlphaChannel.Assign( aBMP );

// Ensure size of alpha channel matches size of image (and is ie8g)
ImageEnView1.IEBitmap.SyncAlphaChannel();

// Update the container
ImageEnView1.Update;

aBMP.free;

Source Image

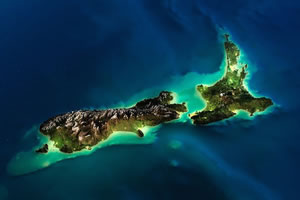
Alpha Image (Black will become transparent, gray will be 50% transparent and white will be fully opaque)

Result (on a white TImageEnView)

Example 2

// Feather the border of a JPEG image
iebmp.Read( 'D:\image.jpg' );
iebmp.AlphaChannel; // Add alpha channel to image
iebmp.Resize(1, 1, 1, 1, clWhite, 0); // Add an alpha border
iebmp.FeatherAlphaEdges(10);

Example 3

// Show the percentage of pixels that are partially or fully transparent
// Same as TImageEnProc.CalcImageNumColors()
var
  px: pbyte;
  y, x, l: integer;
  alphaCount, denom: Integer;
  bmp: TIEBitmap;
begin
  bmp := ImageEnView1.IEBitmap;

  alphaCount := 0;
  if bmp.HasAlphaChannel() then
  begin
    l := IEBitmapRowLen( bmp.AlphaChannel.Width, bmp.AlphaChannel.BitCount, 8);
    for y := 0 to bmp.AlphaChannel.Height - 1 do
    begin
      px := bmp.AlphaChannel.Scanline[y];
      for x := 0 to l - 1 do
      begin
        if px^ < 255 then
          Inc( alphaCount );
        inc(px);
      end;
    end;
  end;

  denom := bmp.Width * bmp.Height;
  ShowMessage( format( 'Image has %d%% transparent pixels', [ Round( alphaCount / denom * 100 )]));
end;

TIEBitmap.AlphaChannel